สวัสดีลูกค้าที่น่ารักทุกท่าน ยินดีต้อนรับทุกท่านเข้าสู่ เว็บหวยออนไลน์ที่ดีที่สุด 999LUCKY155 พร้อมแทงหวยครบวงจรที่ทันสมัยที่สุดในประเทศไทย
สวัสดีลูกค้าทุกๆท่าน ทั้งสมาชิกเก่าและสมาชิกใหม่ของเรา ยินดีต้อนรับทุกท่าน เข้าสู่ระบบ เว็บแทงหวยออนไลน์ 999LUCKY เว็บแทงหวยครบวงจรที่ดีที่สุดอันดับ 1 ในไทยตอนนี้ เว็บหวยออนไลน์ของเรามีอัตราการจ่ายที่สูงที่สุด และยังมีหวยออนไลน์ให้เราได้เลือกเล่นมากมาย อาทิเช่น หวยเวียดนาม หวยรัฐบาล หวยมาเลย์ หวยสิงค์โปร์ หวยลาว huay หวยปิงปอง หวยหุ้นไทย หวยหุ้นประเทศต่างๆ และ หวยลัคกี้เฮง และหวยอื่นๆ และเกมส์ออนไลน์อื่นๆ ให้ท่านได้ร่วมสนุกกันอีกมากมาย
999LUCKY เว็บหวยออนไลน์ จ่ายจริง จ่ายเต็ม จ่ายหนัก อัตราการจ่ายสูง ปรับยอดเครดิตเร็ว โอนไว ถูกล้านจ่ายล้าน ไม่มีโกง แน่นอน 100% เว็บไซต์เราเปิดให้บริการหวยออนไลน์มายาวนานหลายปี โดยที่เราไม่เคยมีประวัติด้านการโกงเลยสักครั้ง จึงทำให้มีลูกค้ามั่นใจและเชื่อถือในเว็บไซต์เราเยอะพอสมควร ลูกค้าส่วนใหญ่ของเราพูดเป็นเสียงเดียวกันว่า 999LUCKY จ่ายจริง การเงิน มั่นคง ปลอดภัย 100%
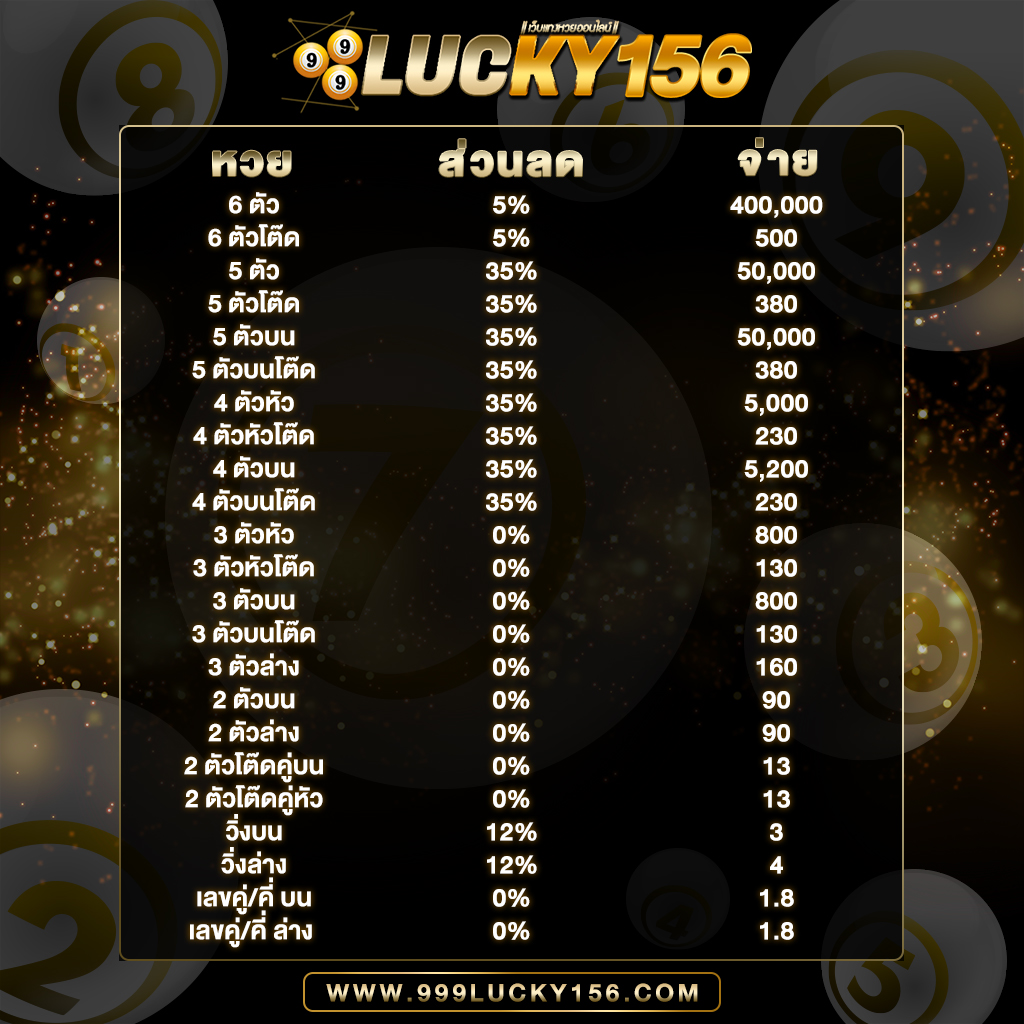
ใครเล่นได้ก็จ่ายตามยอดจริง ไม่มีหัก% ฝากเงินเข้าไปแล้วเล่นได้จริง ถอนเงินออกจากระบบได้รวดเร็วที่สุดในบรรดาเว็บหวย แถมเรายังรองรับ ทุกระบบไม่จะเป็น Android , IOS รวมไปถึงเล่นบน PC , Browser , Windows และทุกระบบเพียงแค่ท่านมีสัญญาณอินเตอร์เน็ต แค่นั้นก็สามารถทำให้ท่านเล่นได้ทุกที่ทุกเวลา ตลอด 24 ชั่วโมง และเรายังมีทีมงานที่มีประสบการณ์สูงคอยให้คำปรึกษาและแก้ไขปัญหาให้ท่านตลอด 24 ซม. การเงิน มั่นคง ปลอดภัย สมัครสมาชิก ต้อง 999LUCKY ที่นี้ที่เดียวเท่านั้น
999LUCKY มาพร้อมระบบรักษาความปลอดภัยขั้นเทพ เซิฟเวอร์คุณภาพสูง เว็บมีความมาตรฐานสูง
- ระบบรักษาความปลอดภัยระดับเทพ
- ใช้ Cloud Server เต็มรูปแบบ
- ระบบ สำรองข้อมูลลูกค้าแบบ Ail Time ไม่ต้องกลัวว่าเงินจะหาย
- ฝากถอนได้โดยไม่มีขั่นต่ำ
- มีโปรโมชั่นและสิทธิพิเศษอีกมากมาย
- แทงหวยไม่มีขั่นต่ำ
- อัตราการจ่ายสูงถึงบาทละ 800
- ระบบฝากถอนอัตโนมัติ รวดเร็ว ทันใจ
- รองรับการแทงหวยออนไลน์เต็มรูปแบบ
- ระบบติดต่อทางทีมงานเราได้ตลอด 24 ซม.
- ระบบแนะนำสมาชิก จ่ายค่าตอบแทนสูงสุดถึง 5%
- หวยปิงปอง ออกผลด้วยตัวเองได้
999LUCKY มั่นใจได้ว่าระบบรักษาความปลอดภัยของเรามาตรฐานอันดับ 1 ในประเทศไทย
- ข้อมูลส่วนตัวและข้อมูลบัญชีของท่านจะถูกปิดบังไว้เป็นความลับเพื่อความปลอดภัยของท่าน
- ความปลอดภัยจากทางบริษัทเราใช้ระบบรักษาความปลอดภัยที่มีสเถียรภาพที่สูง มั่นใจได้ เราจะรักษาความปลอดภัยของท่านไว้อย่างดีแน่นอน
- บริาัทเราเปิดบริการมายาวนานหลายปี จึงมีความน่าเชื่อถือสูง ทำให้ลูกค้าทุกท่านมั่นใจอบอุ่นทุกครั้งที่เข้ามาใช้บริการ
- หากท่านพบเจอปัญหาหรือข้อสวสัย สามารถติดต่อ ฝ่ายบริการลูกค้า ได้ตลอด 24 ซม. แล้วท่านจะคำตอบที่ดีที่สุดจากเรา
- การเงิน ของท่านจะ มั่นคง ปลอดภัยแน่นอน ถ้าเลือกเล่นเว็บหวยออนไลน์ กับ 999LUCKY เว็บหวยออนไลน์ที่ดีที่สุดในประเทศไทย
ข้อดีของการซื้อหวยออนไลน์กับ 999LUCKY
- การเงินท่านจะมั่นคงและปลอดภัย กว่าที่ใดๆ
- เปิดบริการให้เล่นกันยาวๆ ตลอด 24 ซม. ไม่มีปิด
- ซื้อหวยออนไลน์ จ่ายไม่อั้น รับทุกตัว ที่นี้ที่เดียว
- มีทีมงานคุณภาพสูง ที่มากไปด้วยประสบการณคอยดูแลคุณ
- 999LUCKY เว็บเรา ซื่อสัตย์ โปร่งใส่ มั่นใจได้ถ้าเลือกซื้อหวยกับเรา
- ตราจ่ายเยอะที่สุด สูงกว่าเว็บไหนๆ
- แทงเท่าไหร่ ถูกเท่านั้น หลักร้อยหรือหลักล้านเราก็พร้อมจ่าย
- จ่ายจริง จ่ายเต็ม ไม่เคยมีประวัติการโกงมาก่อน ไม่อาเปรียบท่านอย่างแน่นอน
- เว็บเราไม่มีวันหยุดให้บริการ สามารถติดต่อสอบถามเราได้ตลอด 24 ซม.
- มีโปรโมชั่นและโบนัสแจกมากมาย และสิทธิพิเศษอีกมากมาย
เว็บพนันหวยออนไลน์อันดับ 1 ต้อง 999LUCKY เท่านั้น
ซื้อหวยออนไลน์ 999LUCKY จ่ายจริง จ่ายหนัก จ่ายเต็ม จ่ายสูง ราคาดี อัตราจ่ายสูงที่สุด
เว็บได้รับมาตรฐานระดับสากล เซิฟเวอร์คุณภาพสูง มาพร้อมระบบรักษาความปลอดภัยระดับเทพ
ติดต่อทีมงาน 999LUCKY / บริการงานโดย เฮียบิ๊ก @ ปอตเปต
E-Mail : [email protected]
ระบบจะจัดส่งให้ภายในเวลา 2-3 นาทีโดยอัตโนมัติ

